Two Sigma can be a daunting place for new folks. After more than two decades of work, we have amassed a lot of our own language and shorthand. It can be quite confusing trying to keep up with conversations littered with code, jargon, and TLAs.
Epsilon and Omega are two examples of such jargon. They are concepts we use frequently in discussion that are absolutely core to the way we think about how and what we do. Understanding these two related terms can not only help bring new Two Sigma hires up to speed, but can help virtually anyone more clearly define personal and organizational goals, and progress toward them in a rational and systematic way.
If you work at Two Sigma for a while, you will hear people say things like, “This is just an Epsilon” or “What’s your Omega?” But those are shorthand, and they are passed around like a game of telephone, occasionally leading to confusion among the uninitiated.
To borrow a phrase from Elie Wiesel, as the master explained to the disciple who had transposed his verbal teachings to paper: “There is nothing of me in your pages; you thought you heard what I didn’t say.” The goal then, of the next few hundred words is to try and crisply enunciate what we at Two Sigma actually mean when we use the terms Epsilon and Omega.
<aside>
Some history for the curious: The terms Epsilon and Omega were introduced at an annual event called Think Together that ran for several years. A venue where the company could discuss and debate new ideas in business, culture, and process, it was an amazing event for a growing company and served its purpose extremely well. Much of our core culture and many key business ideas emerged as a result of talks given at these events. At the 2012 Think Together, one of our senior engineers (also named Matt) proposed the dual notion of Epsilon and Omega.
Recall that at the time every Google product seemed to be in perpetual beta, the cloud was just beginning to look like the place where you could run software effectively, and many still had CD/DVD drives on their desktops. Most software was still distributed through optical media. But times were changing. Matt’s key observation at Think Together was that, in many ways, the medium defines the message. In an era when software is expensive and time-consuming to deliver to the end-user, software development practices tended to slow down and become very methodical. The last thing you needed was to destroy a run of a million CDs because you found a critical flaw in your software after it was shipped to imaging.
But Google and others changed that. Their incessant betas, Matt posited, were not a slapdash way of pushing out buggy software, but rather a fundamentally new way of delivering software. The medium had changed to a dramatically faster and cheaper distribution mechanism that would have far-reaching consequences for how we engage in every aspect of the software development life-cycle. As a result, he argued, we should change our hypothesis about software development, testing, and distribution to one that is not a staged, discrete graph, but a single, continuous process.
Then, in Two Sigma fashion, Matt asked just a few more questions. What is the calculus of such a process, and where does it lead?
</aside>
As with most things at Two Sigma, face value is not enough, and we always want to keep peeling back layers. I like to say that there are turtles all the way down —predictably scientific (mathematical) ones.

Epsilon was chosen from analysis. If you remember your calculus, then you will be familiar with one version of Epsilon. It’s what we let tend to zero, and thus represents an infinitesimally small amount of measure, and it is critical to helping us define the notion of continuity.
Omega, on the other hand, has the distinction of being the first infinite ordinal number. Given a set of orderable elements, we can talk about the size of the set (its cardinality), and also the ordering of elements in the set (ordinality).
When the set is of finite size, these concepts coincide, and we can use natural numbers to express both cardinality and ordinality. One definition of an ordinal is the set of ordinals that precede it. So that 13 is defined as {0,1,…,12}. In this way, the first infinite ordinal Omega is defined as {0,1,2,….} where the set contains all natural numbers. If each of our Epsilons is an ordinal, then the Omega is defined as the first infinite ordinal that contains all of our Epsilons. It is the goal that we are constantly working towards.
Epsilon and Omega in practice
So there we have it. You understand the history and background to the Two Sigma-isms of Epsilon and Omega. But how are they used? And what is their intent? You might even ask, what is your model here? (And from which we can use the short-hand: what’s your {Epsilon, Omega}?)
An Epsilon is actionable and requires energy, but the Omega is never really attainable, except in the limit–always tantalizingly out of reach.
My model here is geographical. An Omega is the peak of a far mountain. An Epsilon, then, is the smallest reasonable step that you can take that will get you further on your journey than you were before. Much like the frog who leaps half-way to the edge of his pond, an Epsilon is actionable and requires energy, but the Omega is never really attainable, except in the limit–always tantalizingly out of reach.
Just like the peak of a far mountain is clear once seen, an Omega should be simple and crisp to state, once understood. However, understanding the real Omega requires both that you can see through clouds and attendant weather, and also that you are all looking in the right (and same) direction. That means that any Omega should be crisply enunciated (“The Omega for Two Sigma Modeling Engineering is to provide a conversational modeling platform”) and backed up with enough proverbial turtles so that it is well defined.
An Omega is the peak of a far mountain. An Epsilon, then, is the smallest reasonable step that you can take that will get you further on your journey than you were before.
You may have many questions about the Omega:
- What do we mean by “conversational?” (Is the objective zero latency in development, research, etc.?)
- What kind of modeling?
- What kind of platform? (How big/wide, etc.)
But, once clarified, the Omega should suffice.
So, what is an Epsilon? Well, using my “model” above, an Epsilon has two key properties: measure and direction. It needs to have measure; you need to have actually done something that gets you towards the Omega. It also needs a direction. You need to know that you are closer to your Omega. It is this idea of closeness, in any given Omega, that is the most difficult thing to work through.
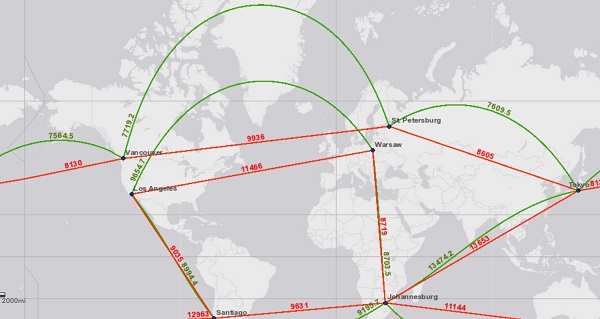
We know that even simple geometric spaces sometimes have confounding notions of distance. That’s why a flight from, say, Vancouver to St. Petersburg might take an extreme northerly route (~7700 km), rather than as-the-crow-flies (~9900 km). The shortest distance curve on a sphere (called a geodesic) is actually along the longitudinal lines.
When your Omega is unclear, direction is hard to find, and even if it is clearly sighted, the journey from here to there may well not be the most seemingly direct route.
Picking a metric is extremely important. And this is where a concise understanding of your Omega becomes critical. If you are misaligned on the Omega, measuring your distance to it is practically impossible. And so a good Omega doesn’t just declare what it is, but also, by inference, what it is not – and this understanding will help you avoid being trapped in a local maxima as you move from Epsilon to Epsilon.
Towers to nowhere
Back to my model. The Omega is to reach the summit high in the distance, and you might be pretty high already, and we know that following a steepest descent algorithm may only find a local maximum. If height is our only concern, then building straight up will do, and is tantalizingly attractive, but we may only end up building a tower to nowhere.
Lest you think that this is all a metaphor, these are very real concerns in building a broad and deep enough platform. Whilst it is true that building a platform does enable you to see further (and solve problems you had not thought of before), if you do end up building a tower to nowhere, the only thing to do, once you realize the problem, may be to climb down, tear down, and rebuild. If indeed the Omega is on the next mountain, then going down is actually a better Epsilon than building up.
A plan is never the Omega, and an Omega is never a plan, but you need one anyway.
To a certain extent, an Epsilon can be construed as a continuous MVP, but it is never shorthand for “the next few sprints,” nor is it continuous improvement in the form of Kaizen, which is a form of gradient descent and presupposes that the process that you already have is as good as it gets.
Figuring out what to put into each Epsilon, how to stage them out, and how to measure progress toward your Omega all require an amalgamation of skills in strategy, design (product and technical), and measurement, along with the ever-present communication and reporting. Getting some of these steps right does not guarantee success, and failing on any of these things ultimately imposes even greater burdens on communication.
Most important, though, is that you have a plan. A plan is never the Omega, and an Omega is never a plan, but you need one anyway. For those still with me and eager to beat this metaphor/model to timely death, I highly recommend watching Free Solo, a remarkable documentary about Alex Honnold’s quest to be the first person to free solo climb El Capitan in Yosemite (widely considered one of the hardest technical climbs in the world). It’s a gripping story, but its purpose in this post is to highlight his plan, Epsilons (represented beautifully in this illustration), and Omega.

Special projects and “the right kind of crazy”
You might be asking where those greenfield, slightly off-the-wall projects that we do on occasion fit into this model (for a small sampling, check out Two Sigma’s open source page). I think that it is fairly straightforward: zero-to-one innovation has the power to drive us toward the Omega in a way that is multiplicative. But it also has a real chance of failure that will set us back two steps (well, actually one; we took a step forward and came to understand what won’t work, and then we took two steps backwards trying to implement it).
So how do we choose these kinds of out-there projects? Well, to borrow a term from Adam Steltzner, a phase lead for the Mars Curiosity Rover (and who spoke here a while back), we are really looking for “the right kind of crazy.” You need to say about the proposed project: yes, this may be slightly off the wall, but if it does succeed, let’s all agree that we would come out above the clouds (to re-beat the metaphor), kind of like digging a tunnel to the top. You might not be sure until you break the surface again whether it will work, although you will be able to measure progress inside the tunnel.
Planning with Omegas and Epsilons
So, as you work on group goals or your own personal objectives, spend some time reflecting over which of them are Omegas (and how you can break them into a coherent, directed set of Epsilons), which are actually Epsilons (and how you infer the Omega from them), and which of your goals are actually just empty carbs (they taste great but ultimately do not further you to any real goal).






